Ciência da Computação UFCG - Uma análise descritiva
Apresentação dos dados
Este documento faz uma análise descritiva e responde algumas perguntas sobre dados referentes a disciplinas da Universidade Federal de Campina Grande (UFCG). Em nosso data frame os dados correspondem aos períodos 2002.1 - 2014.1 em que cada linha representa uma disciplina cursada por um aluno. As principais variáveis que podemos destacar são:
- Matricula: Não a original, mas capaz de identificar cada aluno diferente
- Cod_Curso: Código para identificar cursos diferentes. Cursos com o mesmo nome, mas em campi diferentes são considerados distintos.
- Nome_Curso: Nome do curso.
- Cod_Disciplina: Código para identificar cada disciplina.
- Nome_Disciplina: Nome da disciplina
- Periodo: Período no qual a disciplina foi cursada.
- Media_Disciplina: Média atinginda pelo aluno ao final do período.
- Campus: Campus ao qual o curso pertence.
São listados 95 cursos com códigos diferentes. Abaixo há mais detalhes sobre os dados no geral.
cursos = read.csv("../../../alunosUFCGAnon.csv")
length(unique(cursos$Cod_Curso))## [1] 95summary(cursos)## Matricula Cod_Curso Cod_Disciplina
## B32258 : 143 Min. :11104120 Min. :1105013
## B30701 : 138 1st Qu.:13306200 1st Qu.:1301063
## B22035 : 132 Median :21204100 Median :2101046
## B25585 : 129 Mean :28575038 Mean :2815884
## B27775 : 128 3rd Qu.:41403100 3rd Qu.:4101151
## B28061 : 124 Max. :91402100 Max. :9101274
## (Other):919735
## Cod_Evasao Nome_Curso Periodo
## Min. :0.00000 MEDICINA VETERINÁRIA - D : 60372 Min. :2002
## 1st Qu.:0.00000 MEDICINA - D : 56689 1st Qu.:2008
## Median :0.00000 ENFERMAGEM - D : 53611 Median :2011
## Mean :0.06797 ENGENHARIA CIVIL - D : 42458 Mean :2010
## 3rd Qu.:0.00000 ENGENHARIA ELÉTRICA : 41408 3rd Qu.:2012
## Max. :1.00000 CIÊNCIA DA COMPUTAÇÃO - D: 38246 Max. :2014
## (Other) :627745
## Nome_Disciplina Creditos
## CALCULO DIFERENCIAL E INTEGRAL I : 14822 Min. : 0.00
## ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA: 13091 1st Qu.: 4.00
## FÍSICA GERAL I : 7620 Median : 4.00
## CALCULO DIFERENCIAL E INTEGRAL II : 7285 Mean : 3.89
## METODOLOGIA CIENTÍFICA : 7068 3rd Qu.: 4.00
## LINGUA PORTUGUESA : 6581 Max. :53.00
## (Other) :864062
## Departamento
## UNID. ACAD. DE EDUCAÇÃO : 89211
## UNID. ACAD. DE DIREITO : 73924
## UNID. ACAD. DE MEDICINA VETERINÁRIA : 60320
## UNID. ACAD. DE MATEMÁTICA : 55618
## UNID. ACAD. DE AGRONOMIA E TECNOLOGIA DE ALIMENTO: 38988
## UNID. ACAD. DE SISTEMAS E COMPUTAÇÃO : 36013
## (Other) :566455
## Media_Disciplina Situacao Centro
## Min. : 0.000 Aprovado :751010 Min. :11.00
## 1st Qu.: 6.000 Reprovado : 74289 1st Qu.:13.00
## Median : 7.600 Reprovado por Falta: 69216 Median :21.00
## Mean : 6.789 Trancado : 26014 Mean :28.34
## 3rd Qu.: 8.500 3rd Qu.:41.00
## Max. :10.000 Max. :91.00
## NA's :26042
## Campus Creditos_Curso Tipo
## Min. :1.000 Min. :120.0 Obrigatória:828078
## 1st Qu.:1.000 1st Qu.:204.0 Optativa : 92451
## Median :2.000 Median :240.0
## Mean :2.641 Mean :246.6
## 3rd Qu.:4.000 3rd Qu.:265.0
## Max. :9.000 Max. :526.0
## NA's :3332
## Periodo_Ingresso Periodo_Relativo
## Min. :1995 Min. : 1.000
## 1st Qu.:2007 1st Qu.: 2.000
## Median :2009 Median : 4.000
## Mean :2009 Mean : 4.231
## 3rd Qu.:2011 3rd Qu.: 6.000
## Max. :2014 Max. :28.000
## Em quais cursos estão as melhores e piores notas? Por que você acha que isso acontece em cada caso?
Existem duas maneiras principais e diretas de avaliar quais são os cursos com melhores e piores notas, pelo cáclculo de média ou mediana. Devido a quantidade muito variada de alunos em cada curso, escolhemos responder esta pergunta utilizando a mediana, dessa forma o valor não será afetado por outliers.
Para cada curso, foi calculada a mediana sobre todas as médias de disciplinas dos alunos, desconsiderando valores vazios. Abaixo temos dois gráficos que, de maneira ordenada, exibe os dez melhores e piores cursos com relação a médias em disciplinas.
cursos = cursos[!is.na(cursos$Media_Disciplina),]
cursos_mediana = aggregate(cursos$Media_Disciplina, list(cursos$Cod_Curso, cursos$Nome_Curso, cursos$Campus), FUN = median)
cursos_mediana = cursos_mediana[ order( cursos_mediana$x),]
ggplot(cursos_mediana[1:10,], aes( y = x, x = reorder(Group.2, -x), fill=factor(Group.3))) + geom_bar(position="dodge", stat="identity") + geom_text(aes(label=x),size = 4) + coord_flip() + labs(title = "Cursos com piores notas", x = "Curso", y = "Mediana", fill = "Campus")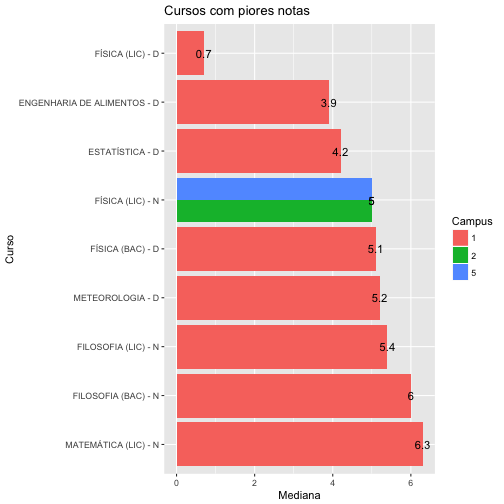
ggplot(cursos_mediana[86:95,], aes( y = x, x = reorder(Group.2, -x),, fill=factor(Group.3))) + geom_bar(stat="identity", position="dodge") + geom_text(aes(label=x),size = 4) + coord_flip() + labs(title = "Cursos com melhores notas", x = "Curso", y = "Mediana", fill = "Campus")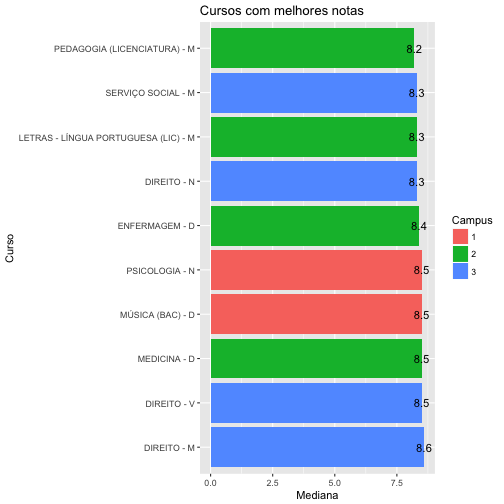
Segundo os gráficos acima, podemos concluir que, com mediana igual a 0.7, o curso FÍSICA (LIC) - D é considerado aquele com piores notas, enquanto DIREITO - M, com mediana igual a 8.6, é considerado aquele com melhores notas. O curso de Física pertence ao campus 1 e o de direito ao campus 3.
unique(cursos[cursos$Cod_Curso == cursos_mediana[1,]$Group.1,]$Campus)## [1] 1unique(cursos[cursos$Cod_Curso == cursos_mediana[95,]$Group.1,]$Campus)## [1] 3Esse resultado pode ser afetado de diversas maneiras. Nos dados utilizados para essa análise, para o curso de direto temos mais de 23000 valores enquando física não chega a 700. Em casos desse tipo a quantidade de desistentes ou reprovações tem um efeito maior no grupo de menor valor. Além do mais, podemos ver no boxplot abaixo que para o curso de direito as notas estão bem concentradas em altos valores e apesar de apresentar outliers, estes não exercem influência. Por outro lado, as notas do curso de física têm uma maior variabilidade e concentração de baixos valores valores.
ggplot(cursos[cursos$Cod_Curso == 11105110 | cursos$Cod_Curso == 31350100,], aes( y = Media_Disciplina, x = Nome_Curso)) + geom_boxplot() + labs(title = "DIREITO - M x FÍSICA (LIC) - D", x = "Curso", y = "Média")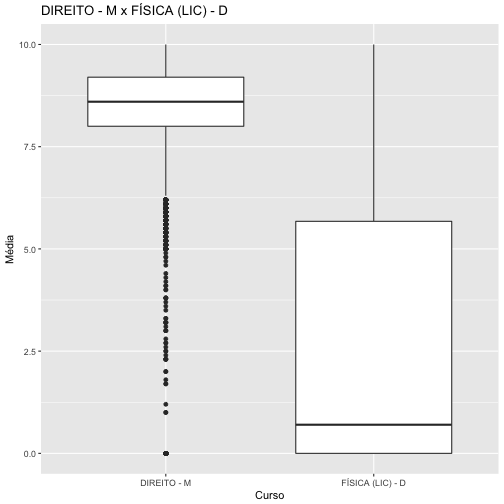
Em qual período estão as melhores e piores notas do curso de Ciência da Computação?
Seguindo o mesmo procedimento adotado na questão anterior, agora agrupamos as médias por período. Porém, no gráfico abaixo é possível identificar um problema na definição de melhor e pior período. Ao verificar a mediana dos últimos períodos, vemos que todos pussuem o mesmo valor e variabilidade semelhante, impossibilitando escolher apenas um.
ccc_medias = subset(cursos, Cod_Curso == 14102100)
ggplot(ccc_medias, aes(factor(Periodo), Media_Disciplina )) + geom_boxplot() + labs(title = "Notas de CC por período", x = "Período", y = "Nota") + theme(axis.text.x = element_text(angle = 90, hjust = 1))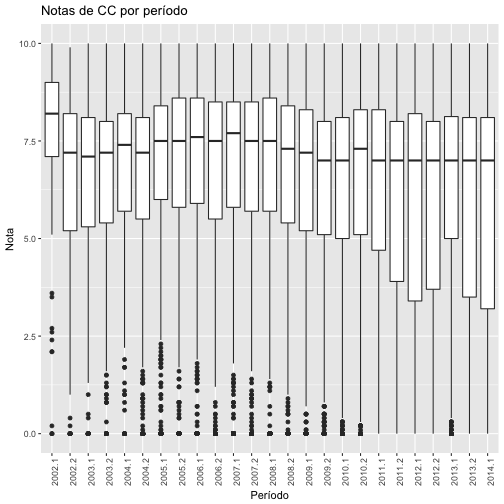
Para contornar esse problema, vamos analisar os perídos a partir do cálculo das médias. No gráfico abaixo estão marcadas as médias das notas de cada período. Observamos que, assim como no boxplot anterior, o período 2002.1 permanece no topo com melhores notas. Por outro lado, vemos diferenças nos valores referentes aos últimos períodos que antes estavam iguais. Com um pequena diferença para 2012.1, 2014.1 apresentas a média mais baixa de notas, sendo considerado então o de piores notas.
ccc_medias = aggregate(ccc_medias$Media_Disciplina, list(ccc_medias$Periodo), FUN = mean, na.rm=TRUE)
ggplot(ccc_medias, aes( y = x, x =factor( Group.1), group = 1)) + geom_line(color = "#d94801") + geom_point(size = 2, color = "#8c2d04") + labs(title = "Médias de notas de CC por período", x = "Período", y = "Média") + theme(axis.text.x = element_text(angle = 90, hjust = 1))
Existe correlação entre as notas de Matemática Discreta e Cálculo I para o curso de Ciência da Computação? Se sim, a correlação é positiva ou negativa? Qual a força dessa correlação?
Para esta análise serão considerados apenas as notas de pessoas que cursaram as disciplinas Matemática Discreta e Cálculo I, em outras palavras, apenas quando houver notas disponíveis referentes as duas disciplinas ligeada a uma só matrícula. Para casos de quando há mais de uma nota para as disciplinas, apenas a maior é considerada.
Após realizado o filtro e recortes adequados, plotamos abaixo um gráfico em que as notas de Cálculo I estão representadas no eixo X e as notas de Matemática Discretas estão representadas no eixo Y. Observamos que há um tipo de marcação na imagem gerada, exatamente onde as notas atingem o valor 5. Os pontos anteriores a estar marcação estão bem dispersos, enquanto os após a marcação se encontram mais concentrados em na região direita superior.
discreta = subset(cursos, Cod_Disciplina == 1109113) %>% group_by(Matricula) %>% top_n(1, Media_Disciplina)
calculo = subset(cursos, Cod_Disciplina == 1109103) %>% group_by(Matricula) %>% top_n(1, Media_Disciplina)
disc = subset(discreta, select = c("Matricula", "Media_Disciplina"))
calc = subset(calculo, select = c("Matricula", "Media_Disciplina"))
disc.calc = merge(calc,disc, by.x = "Matricula", by.y = "Matricula")
ggplot(disc.calc, aes(Media_Disciplina.x, Media_Disciplina.y)) + geom_point(alpha = 0.5, color = "#7a0177") + labs(title = "Relação de notas Cálculo I x Matemática Discreta", x = "Notas de Cálculo I", y = "Notas de Matemática Discreta") + geom_smooth(method = lm)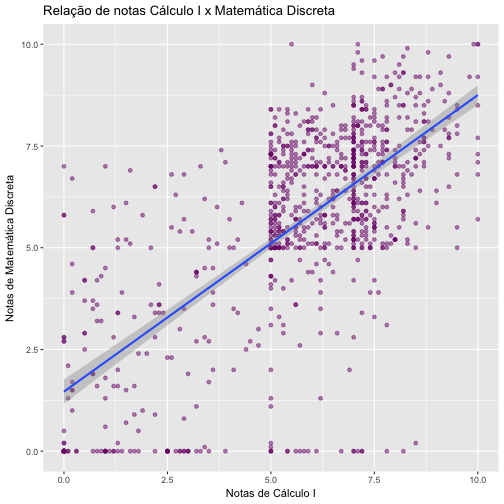
Apesar de um pouco disperso, no gráfico acima os pontos se desenham de maneira em é possível observar uma tendência. Desconsiderando outliers, vemos que a dendência é de que as notas de ambas as disciplinas geralmente crescem juntas. Esse é um indicativo de que há correlação entre as duas variáveis. Abaixo temos o valor da correlação calculado:
cor(disc.calc$Media_Disciplina.x, disc.calc$Media_Disciplina.y)## [1] 0.6927944Seu valor é igual a 0.6927944 e por ser diferente de zero podemos afirmar que há correlação. Um valor acima de 0 significa que essa correlação é possitiva. Quanto mais próximo de 1 ou -1, maior a força. Sendo nosso valor quase 0.70, podemos considerar que há uma forte correlação positiva.