Laboratório 3 - Parte 2
knitr::opts_chunk$set(screenshot.force = FALSE)Esta é a continuação do laboratório 3. Aqui damos continuidade ao tema “evasão no primeiro período”. Na parte 1 foi feita a análise descritiva dos dados, nesta parte 2 estaremos utilizando algoritmos de classificação para tentar prever evasão de alunos no curso de computação ao fim do primeiro período.
Separação dos dados em treino e teste
A utilização dos dados será feita a partir do ano 2011, já que é a partir desse ano que se observa um aumento considerável no número de matrículas, enquanto o número de evasões permanece semelhante nos anos seguintes.
dados = read.csv("treino_classificacao_v2.csv")
mat_unicas = dados[!duplicated(dados[,1]),]
contagem.distr = group_by(mat_unicas, MAT_TUR_ANO, EVADIU) %>% summarise(count = n())
hchart(contagem.distr, "column", hcaes(x = MAT_TUR_ANO, y = count, group = EVADIU), name= c('Não evadiu', "Evadiu")) %>% hc_title(text = "Distribuição das classes") %>% hc_colors(c("darkblue", "orange")) %>% hc_yAxis(title = list(text = "Total de alunos")) %>% hc_xAxis(title = list(text = "Ano"))plot of chunk unnamed-chunk-2
Desses dados, os dividimos em treino e teste. Os dados de teste serão aqueles referentes as matrículas realizadas em 2015.2, o resto dos dados a partir de 2011 irão compor os dados de treino.
dados.treino = subset(dados, MAT_TUR_ANO > 2010 & (MAT_TUR_ANO < 2015))
dados.treino = rbind(dados.treino, subset(dados, MAT_TUR_ANO == 2015 & MAT_TUR_PERIODO == 1))
dados.teste = subset(dados, MAT_TUR_ANO == 2015 & MAT_TUR_PERIODO == 2)
dados.treino = dados.treino %>% select(-MAT_TUR_DIS_DISCIPLINA, -MAT_TUR_ANO, -MAT_TUR_PERIODO) %>% filter(!is.na(MAT_MEDIA_FINAL))
dados.teste = dados.teste %>% select(-MAT_TUR_DIS_DISCIPLINA, -MAT_TUR_ANO, -MAT_TUR_PERIODO) %>% filter(!is.na(MAT_MEDIA_FINAL))
alunos.evadiu.treino = dados.treino %>%
group_by(MAT_ALU_MATRICULA) %>%
summarise(evadiu = any(EVADIU))
alunos.evadiu.teste = dados.teste %>%
group_by(MAT_ALU_MATRICULA) %>%
summarise(evadiu = any(EVADIU))
dados.treino = dados.treino %>%
group_by(MAT_ALU_MATRICULA, disciplina) %>%
filter(MAT_MEDIA_FINAL == max(MAT_MEDIA_FINAL)) %>%
ungroup() %>%
select(MAT_ALU_MATRICULA, disciplina, MAT_MEDIA_FINAL) %>%
mutate(disciplina = as.factor(gsub(" ",".",disciplina))) %>%
dcast(MAT_ALU_MATRICULA ~ disciplina, mean) %>%
merge(alunos.evadiu.treino)
dados.teste = dados.teste %>%
group_by(MAT_ALU_MATRICULA, disciplina) %>%
filter(MAT_MEDIA_FINAL == max(MAT_MEDIA_FINAL)) %>%
ungroup() %>%
select(MAT_ALU_MATRICULA, disciplina, MAT_MEDIA_FINAL) %>%
mutate(disciplina = as.factor(gsub(" ",".",disciplina))) %>%
dcast(MAT_ALU_MATRICULA ~ disciplina, mean) %>%
merge(alunos.evadiu.teste)Adicionando atributos
Percebemos que algumas notas de disciplinas estão com valores vazios. Para que não precisemos remover toda a linha do data frame, vamos realizar imputação de dados. Decidimos que os valores vazios em disciplinas serão substituídos pelo valor da média das notas presentes.
for(i in 1:nrow(dados.treino)){
for(j in 1:ncol(dados.treino)){
if(is.na(dados.treino[i,j])){
dados.treino[i, j] = sum(dados.treino[i,2:7], na.rm = T)/(6-sum(is.na(dados.treino[i,2:7])))
}
if(i <= nrow(dados.teste)){
if(is.na(dados.teste[i,j])){
dados.teste[i, j] = sum(dados.treino[i,2:7], na.rm = T)/(6-sum(is.na(dados.treino[i,2:7])))
}
}
}
}
head(dados.treino)## MAT_ALU_MATRICULA
## 1 0044fe18610b0e666a8630b6b7f98386
## 2 0049c0b6a2e2db661f8e15e7bc2b7581
## 3 0134dc0b387e4dff42a0d2b45423564b
## 4 0189d03cbf10376083a4a70ec39dab90
## 5 01cb852b7b7bc76cc99e7f32376d7166
## 6 02188304b2556b3bd0a6a4f4bc2/f1f4d
## Álgebra.Vetorial.e.Geometria.Analítica
## 1 9.4
## 2 1.0
## 3 7.8
## 4 2.0
## 5 7.0
## 6 3.8
## Cálculo.Diferencial.e.Integral.I Introdução.à.Computação
## 1 8.5 8.8
## 2 0.7 8.6
## 3 6.3 8.0
## 4 3.8 5.3
## 5 0.0 5.0
## 6 3.4 7.2
## Laboratório.de.Programação.I Leitura.e.Produção.de.Textos
## 1 8.4 9.30
## 2 8.8 5.54
## 3 8.4 7.76
## 4 5.1 7.40
## 5 3.8 7.50
## 6 7.4 7.80
## Programação.I evadiu
## 1 8.3 FALSE
## 2 8.6 FALSE
## 3 8.3 FALSE
## 4 5.1 FALSE
## 5 3.8 FALSE
## 6 7.4 FALSEPara um novo atributo, decidimos que será uma variável categórica chamada Programacao. Se o aluno reprovou Programação I ou Lab. de Programação I, o valor será TRUE, caso contrário, FALSE.
dados.treino$Programacao[dados.treino$Programação.I >= 5 & dados.treino$Laboratório.de.Programação.I >= 5 ] = F
dados.teste$Programacao[dados.teste$Programação.I >= 5 & dados.teste$Laboratório.de.Programação.I >= 5 ] = F
dados.treino$Programacao[is.na(dados.treino$Programacao)] = T
dados.teste$Programacao[is.na(dados.teste$Programacao)] = TTreino - Modelos de regressão logística
set.seed(123)
dados.treino$evadiu = as.factor(dados.treino$evadiu)
dados.teste$evadiu = as.factor(dados.teste$evadiu)
dados.treino$Programacao = as.factor(dados.treino$Programacao)
dados.teste$Programacao = as.factor(dados.teste$Programacao)
model.gml = train(evadiu ~. -MAT_ALU_MATRICULA,
data=dados.treino,
method="glm",
family="binomial")Treino - Modelos de árvore de decisão
Tivemos que substituir os valores da variável criada por valores numéricos porque a função de criar o modelo não estava aceitando a variável caregórica.
dtf2 = select(dados.treino, -Programacao)
dtf2$Programacao[dados.treino$Programacao==T] = 1
dtf2$Programacao[dados.treino$Programacao==F] = 0
model.tree = rpart(evadiu ~ . -MAT_ALU_MATRICULA, data=dtf2)Interpretação de coeficientes da regressão
Vemos abaixo que as variáveis mais significativas são Leitura.e.Produção.de.Texto e Introdução.à.Computação. Essas variáveis apresentam os menores p-valores, o que para mim não faz muito sentido. Talvez essa importância seja resultado da imputação dos dados.
summary(model.gml)##
## Call:
## NULL
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.0043 -0.2656 -0.2042 -0.1575 2.9912
##
## Coefficients:
## Estimate Std. Error z value
## (Intercept) 2.44665 1.24505 1.965
## Álgebra.Vetorial.e.Geometria.Analítica 0.14095 0.12996 1.085
## Cálculo.Diferencial.e.Integral.I -0.02382 0.11934 -0.200
## Introdução.à.Computação -0.27365 0.13146 -2.082
## Laboratório.de.Programação.I 0.22050 0.42583 0.518
## Leitura.e.Produção.de.Textos -0.63918 0.14586 -4.382
## Programação.I -0.20915 0.40949 -0.511
## ProgramacaoTRUE 0.45035 0.83894 0.537
## Pr(>|z|)
## (Intercept) 0.0494 *
## Álgebra.Vetorial.e.Geometria.Analítica 0.2781
## Cálculo.Diferencial.e.Integral.I 0.8418
## Introdução.à.Computação 0.0374 *
## Laboratório.de.Programação.I 0.6046
## Leitura.e.Produção.de.Textos 1.18e-05 ***
## Programação.I 0.6095
## ProgramacaoTRUE 0.5914
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 362.94 on 575 degrees of freedom
## Residual deviance: 194.56 on 568 degrees of freedom
## AIC: 210.56
##
## Number of Fisher Scoring iterations: 6Acurácia, precision e recall no treino e teste
- TP: true-positive;
- TN: true-negative;
- FP: false-positive;
-
FN: false-negative.
- Acurácia: proporção de observações corretamente classificadas. (TP+TN)/(TP+TN+FP+FN);
- Precisão: quantas das observaçoes preditas como positivas são realmente positivas. TP/(TP+FP);
- Recall: quantas observaçoes positivas foram corretamente classificadas. TP/(TP+FN).
Regressão logística
dados.teste$predicao.gml = predict(model.gml, dados.teste)
temp = dados.teste %>% select(evadiu, predicao.gml)
TP = subset(temp, evadiu == TRUE & predicao.gml == TRUE) %>% nrow()
TN = subset(temp, evadiu == FALSE & predicao.gml == FALSE) %>% nrow()
FP = subset(temp, evadiu == FALSE & predicao.gml == TRUE) %>% nrow()
FN = subset(temp, evadiu == TRUE & predicao.gml == FALSE) %>% nrow()Vemos abaixo que a acurácia do modelo parece boa, mais de 90% das previsões foram realizadas corretamente. Porém, os valores de precisão e recall são bem mais baixos. Com precisão igual a 0.5 siginifica que em metade das vezes foi prevista uma evasão quando não ocorreu. Com o valor de Recall aproximadamente igual a 0.57 significa que o modelo só preveu 57% dos alunos que evadiram. Essa característica se deve ao fato de que as classes estão desbalanceadas.
## [1] "Acurácia: 0.923913043478261"## [1] "Precisão: 0.5"## [1] "Recall: 0.571428571428571"Árvore de decisão
tst2 = select(dados.teste, -Programacao)
tst2$Programacao[dados.teste$Programacao==T] = 1
tst2$Programacao[dados.teste$Programacao==F] = 0
predicao.tree = as.data.frame(predict(model.tree, tst2))
temp = apply(predicao.tree['TRUE'], 2, FUN = function(x){return(x > 0.5)})
tst2$predicao.tree = as.factor(temp)
temp = tst2 %>% select(evadiu, predicao.tree)
TP = subset(temp, evadiu == TRUE & predicao.tree == TRUE) %>% nrow()
TN = subset(temp, evadiu == FALSE & predicao.tree == FALSE) %>% nrow()
FP = subset(temp, evadiu == FALSE & predicao.tree == TRUE) %>% nrow()
FN = subset(temp, evadiu == TRUE & predicao.tree == FALSE) %>% nrow()Vemos abaixo que a acurácia do modelo parece boa, mais de 90% das previsões foram realizadas corretamente. Porém, não foi possível calcular a precisão, dado que, como não houve nenhuma ocorrência de valores TP e FP, não é possível realizar uma divisão por zero. De maneira análoga, o valor de Recall foi igual a zero, dado que TP também é igual a zero, implicando que o modelo não conseguiu prever a evasão de nenhum aluno. Mais uma vez, essa característica se deve ao fato de que as classes estão desbalanceadas e quando isso ocorre a acurácia do modelo será enganadora.
## [1] "Acurácia: 0.923913043478261"## [1] "Precisão: NaN"## [1] "Recall: 0"Controle overfitting usando validação-cruzada
Regressão Logistica
Ridge
O modelo de regressão para ridge é ajustado chamando a função glmnet com alpha igual a 0. Glmnet desenvolve modelos em uma grade com cerca de 100 valores de lambda, como podemos ver no gráfico abaixo. Quando log de lambda é 4, todos os coeficientes são essencialmente zero. Então, à medida que relaxamos lambda, os coeficientes crescem de distanciando de zero.
set.seed(123)
model.ridge = glmnet(x = model.matrix( ~ . -MAT_ALU_MATRICULA -evadiu, dados.treino),
y = dados.treino$evadiu,
alpha = 0,
family = 'binomial')
plot(model.ridge, xvar = "lambda", label = T)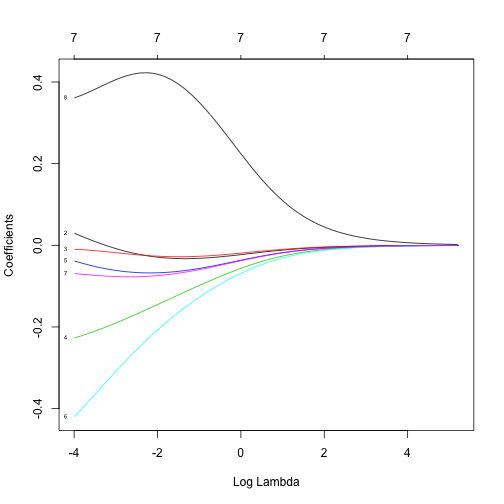
Para selecionar um modelo ridge executamos a função cv.glmnet que fará validação cruzada. Na parte superior do gráfico é possível ver quantos coeficientes de variáveis não-zero estão no modelo. Há todas as 7 variáveis no modelo, 6 variáveis e o intercept, e nenhum coeficiente é zero.
No início, o desvio binomial é mais alto e os coeficientes são pequenos até que, em algum ponto, ele se eleva e o intervalo é reduzido.
cv.ridge = cv.glmnet(model.matrix( ~ . -MAT_ALU_MATRICULA -evadiu, dados.treino), y=dados.treino$evadiu, alpha=0, family="binomial")
plot(cv.ridge, sub = T)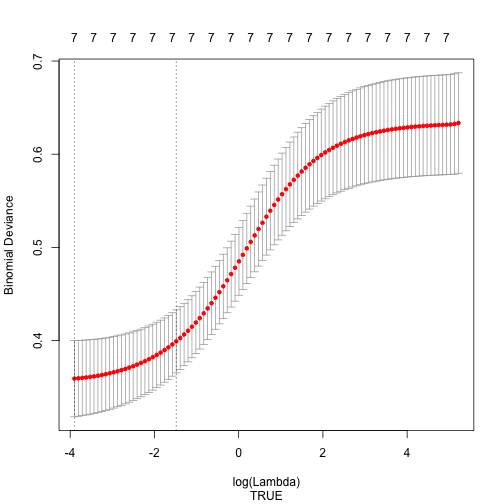
Lasso
O modelo de regressão para lasso é ajustado chamando a função glmnet com alpha igual a 1.
set.seed(123)
model.lasso = glmnet(x = model.matrix( ~ . -MAT_ALU_MATRICULA -evadiu, dados.treino),
y = dados.treino$evadiu,
alpha = 1,
family = 'binomial')
plot(model.lasso, xvar = "lambda", label = T)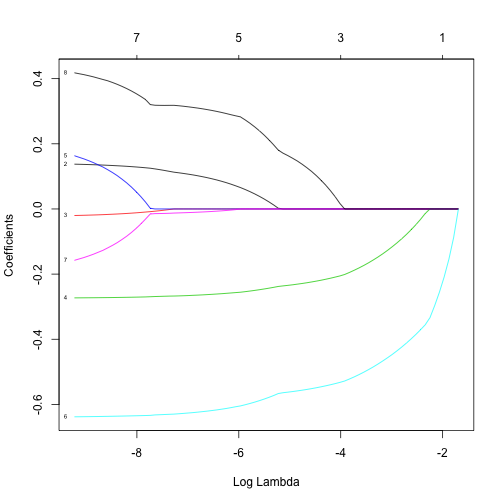
O plot tem várias opções, o desvio, por exemplo, está relacionado fraction deviance explained, que é equivalente a r-quadrado em regressão. Notamos que muito do r-quadrado foi explicado por basicamente duas variáveis, representadas pelas cores verde e azul claro.
plot(model.lasso,xvar="dev",label=TRUE)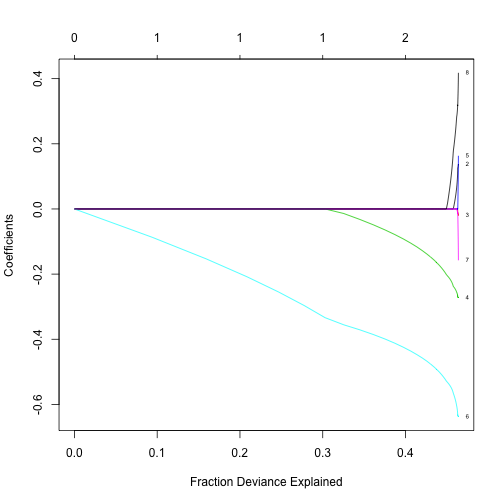
Coeficientes podem ser extraídos do glmmod. Aqui mostrado com 2 variáveis selecionadas. sendo elas Introdução.à.Computação e Leitura.e.Produção.de.Textos. Decidimos então que o melhor modelo para regressão logística será composto apenas por essas duas variáveis intependentes.
coef(model.lasso)[,10]## (Intercept)
## 0.56035148
## (Intercept)
## 0.00000000
## Álgebra.Vetorial.e.Geometria.Analítica
## 0.00000000
## Cálculo.Diferencial.e.Integral.I
## 0.00000000
## Introdução.à.Computação
## -0.04883549
## Laboratório.de.Programação.I
## 0.00000000
## Leitura.e.Produção.de.Textos
## -0.38557798
## Programação.I
## 0.00000000
## ProgramacaoTRUE
## 0.00000000Assim como em ridge, realizamos o processo para visualização da validação cruzada.
cv.lasso = cv.glmnet(model.matrix( ~ . -MAT_ALU_MATRICULA -evadiu, dados.treino), y=dados.treino$evadiu, alpha=1, family="binomial")
plot(cv.lasso)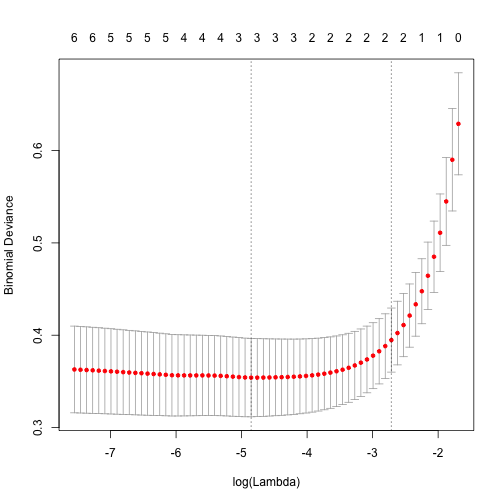
E definimos o novo melhor modelo de regressão logística.
set.seed(123)
fitControl = trainControl(method = "cv", number = 10)
best.glm.model = model.lasso = train(evadiu ~ Introdução.à.Computação + Leitura.e.Produção.de.Textos,
data=dados.treino,
method="glm",
family="binomial",
preProcess = c('scale', 'center'),
trControl = fitControl,
na.action = na.omit)Árvore de decisão
Para a árvore de decisão, é utilizada a função rpart.control, definindo um valor máximo de altura igual a 30 (valor recomendado).
dt.control = rpart.control(maxdepth=30)
model.tree = rpart(evadiu ~ . -MAT_ALU_MATRICULA,
data=dtf2,
method="class",
control=dt.control)
printcp(model.tree)##
## Classification tree:
## rpart(formula = evadiu ~ . - MAT_ALU_MATRICULA, data = dtf2,
## method = "class", control = dt.control)
##
## Variables actually used in tree construction:
## [1] Introdução.à.Computação Leitura.e.Produção.de.Textos
##
## Root node error: 55/576 = 0.095486
##
## n= 576
##
## CP nsplit rel error xerror xstd
## 1 0.509091 0 1.00000 1.00000 0.128241
## 2 0.018182 1 0.49091 0.50909 0.093842
## 3 0.010000 2 0.47273 0.58182 0.099954best.tree = prune(model.tree,
+ model.tree$cptable[which.min(model.tree$cptable[,"xerror"]),"CP"])Acurácia, precision e recall da validação-cruzada e teste (para os melhores modelos)
Regressão Logística
dados.teste$best.glm.prediction = predict(best.glm.model, dados.teste)
temp = dados.teste %>% select(evadiu, best.glm.prediction)
TP = subset(temp, evadiu == TRUE & best.glm.prediction == TRUE) %>% nrow()
TN = subset(temp, evadiu == FALSE & best.glm.prediction == FALSE) %>% nrow()
FP = subset(temp, evadiu == FALSE & best.glm.prediction == TRUE) %>% nrow()
FN = subset(temp, evadiu == TRUE & best.glm.prediction == FALSE) %>% nrow()Comparando com o modelo anterior de regressão logística, vemos que ambos os modelos apresentam os mesmos valores para acurácia, precisão e recall. Isso significa que o novo modelo não é pior, mas também não é melhor.
## [1] "Acurácia: 0.923913043478261"## [1] "Precisão: 0.5"## [1] "Recall: 0.571428571428571"Árvore de decisão
predicao.best.tree = as.data.frame(predict(best.tree, tst2))
temp = apply(predicao.best.tree['TRUE'], 2, FUN = function(x){return(x > 0.5)})
tst2$predicao.best.tree = as.factor(temp)
temp = tst2 %>% select(evadiu, predicao.best.tree)
TP = subset(temp, evadiu == TRUE & predicao.best.tree == TRUE) %>% nrow()
TN = subset(temp, evadiu == FALSE & predicao.best.tree == FALSE) %>% nrow()
FP = subset(temp, evadiu == FALSE & predicao.best.tree == TRUE) %>% nrow()
FN = subset(temp, evadiu == TRUE & predicao.best.tree == FALSE) %>% nrow()Já para o novo modelo de árvore de decisão, o valor de acurácia teve uma leve reduzida, mas ainda se mantém acima dos 90%. Por outro lado, agora é possível calcular um valor de precisão, que agora se apresenta em aproximadamente 0.45. O recall que antes era zero, foi alterado para 0.71. Vemos uma melhora considerável nesse novo modelo de árvore de decisão.
## [1] "Acurácia: 0.91304347826087"## [1] "Precisão: 0.454545454545455"## [1] "Recall: 0.714285714285714"Aplicação do melhor modelo
Consideramos como melhor modelo o modelo de árvore de regressão melhorado, alguns dos motivos são:
- Não podemos considerar o valor da acurária dado que os dados estão muito desbalanceados.
- Neste caso, o Recall é o que utilizamos para considerar o melhor modelo. É muito mais importante identificar alunos que vão evadir, classificar como false um aluno que vai evadir é considerado uma grande perda.
- Classificar como true um aluno que na verdade não vai evadir não implicará em grande impactos.
pessoal.dados = data.frame(MAT_ALU_MATRICULA="0674a56175b24881b769d167a199cb41", Álgebra.Vetorial.e.Geometria.Analítica = 7.3, Cálculo.Diferencial.e.Integral.I = 5.5, Introdução.à.Computação=8.4, Laboratório.de.Programação.I = 7.7, Leitura.e.Produção.de.Textos = 8.2, Programação.I = 7.6, evadiu = F, Programacao = 0)
pessoal.predicao = as.data.frame(predict(best.tree, pessoal.dados))
temp = apply(pessoal.predicao['TRUE'], 2, FUN = function(x){return(x > 0.5)})
pessoal.predicao = as.factor(temp)
pessoal.predicao## TRUE
## FALSE
## Levels: FALSEComo resultado para os dados pessoais, o modelo fez a predição correta a meu respeito.