Uso de Regrassão Logística
Apresentação dos dados
Nesse laboratório utilizamos dados referentes aos alunos que já concluíram o curso de Ciência da Computação - UFCG. Nele se encontram, de cada aluno, todas as médias finais obtidas em cada disciplina (5-10), assim como o coeficiente de rendimento acadêmico (cra, ~4-10).
Queremos realizar análises de regressão utilizando as disciplinas dos dois primeiros períodos e cra na tentativa de responder a seguinte pergunta:
O desempenho dos alunos nos dois primeiros períodos consegue explicar, em algum grau, seus desempenhos no curso como um todo?
Para isso, construiremos um modelo de regressão com disciplinas do primeiro e segundo período. Ao longo desse documento iremos responder perguntas a respeito do modelo e realizar comparações. Logo abaixo um breve resumo de como se distribuem as variáveis quando relacionadas e seus respectivos coeficientes de correlação.
Legenda
- Cálculo.1: Cálculo Diferencial e Integral I - Período 1
- Vetorial: Álgebra Vetorial e Geometria Analítica - Período 1
- LPT: Leitura e Produção de Textos - Período 1
- P1: Programação I - Período 1
- LP1: Laboratório de Programação I - Período 1
- IC: Introdução à Computação - Período 1
- Cálculo.2: Cálculo Diferencial e Integral II - Período 2
- Discreta: Matemática Discreta - Período 2
- P2: Programação II - Período 2
- LP2: Laboratório de Programação II - Período 2
- Grafos: Teoria dos Grafos - Período 2
- Física.3: Fundamentos de Física Clássica - Período 2
graduados = read.csv("graduados_disciplinas.csv")
graduados = graduados[, c("Cálculo.Diferencial.e.Integral.I", "Álgebra.Vetorial.e.Geometria.Analítica", "Leitura.e.Produção.de.Textos", "Programação.I", "Laboratório.de.Programação.I", "Introdução.à.Computação", "Cálculo.Diferencial.e.Integral.II", "Matemática.Discreta", "Programação.II", "Laboratório.de.Programação.II", "Teoria.dos.Grafos", "Fundamentos.de.Física.Clássica", "cra")]
colnames(graduados) = c("Cálculo.1", "Vetorial", "LPT", "P1", "LP1", "IC", "Cálculo.2", "Discreta", "P2", "LP2", "Grafos", "Física.3", "cra")
ggpairs(na.omit(graduados), lower = list(continuous = "smooth"), upper = list(continuous = wrap("cor", size = 10)))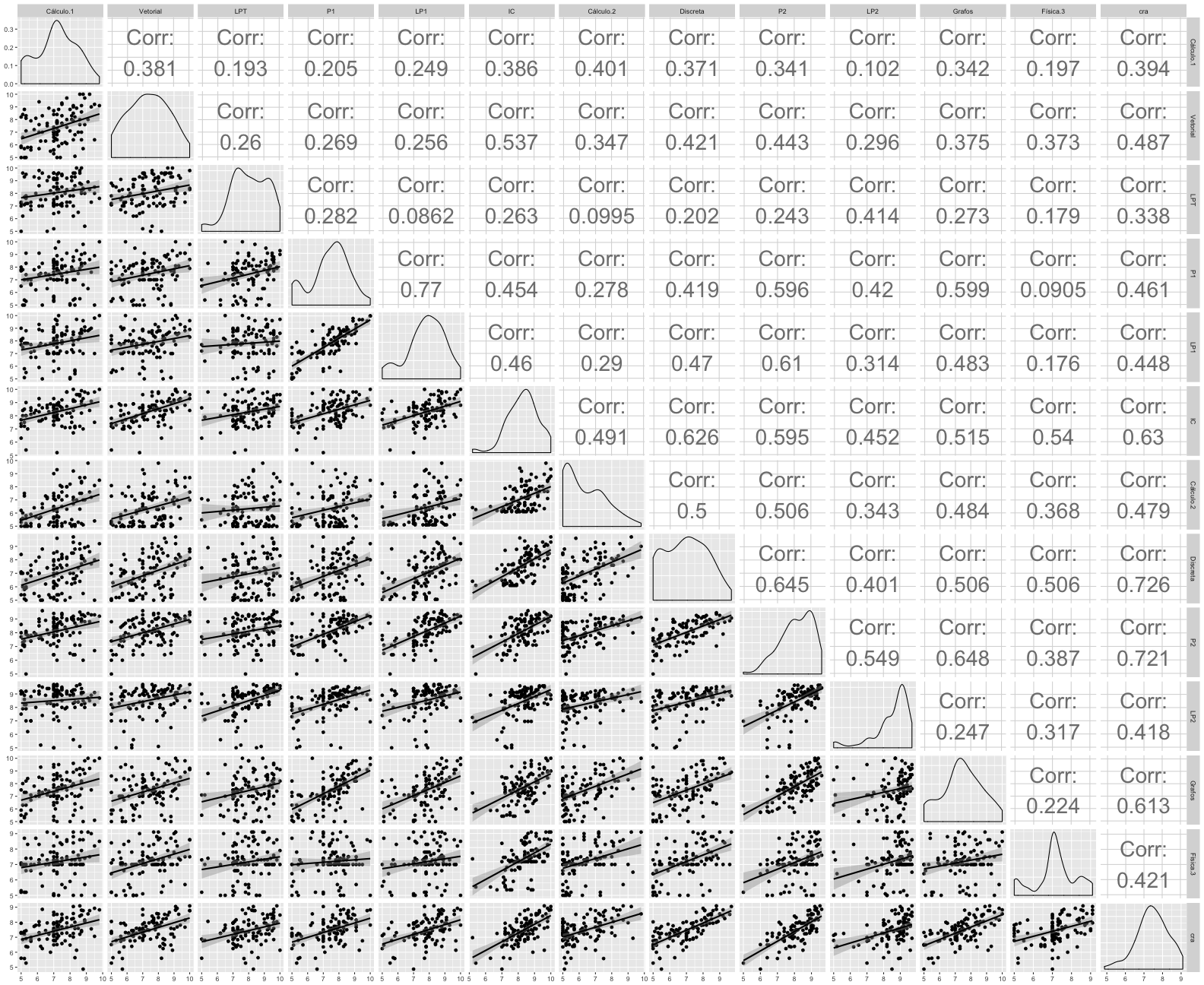
Um modelo de regressão múltipla com todas as variáveis é plausível para explicar a variação em y? Em que grau?
Para responder esta pergunta criamos um modelo de regressão linear múltipla que englobe todas disciplinas como variáveis independentes e o cra como variável dependente. Após a criação do modelo, obtemos um resumo do mesmo com suas principais características relacionadas a efetividade.
rl = lm(cra ~ ., data = graduados)
summary(rl)##
## Call:
## lm(formula = cra ~ ., data = graduados)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.8273 -0.2988 0.1069 0.2796 1.0032
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.33894 0.59783 2.240 0.02758 *
## Cálculo.1 0.02121 0.04907 0.432 0.66661
## Vetorial 0.04443 0.04762 0.933 0.35327
## LPT 0.09172 0.05167 1.775 0.07925 .
## P1 -0.02593 0.07684 -0.337 0.73660
## LP1 -0.02472 0.07450 -0.332 0.74082
## IC 0.10196 0.08639 1.180 0.24098
## Cálculo.2 -0.00100 0.05302 -0.019 0.98499
## Discreta 0.23935 0.05863 4.083 9.63e-05 ***
## P2 0.29214 0.09553 3.058 0.00293 **
## LP2 -0.02848 0.06666 -0.427 0.67024
## Grafos 0.09620 0.06302 1.526 0.13040
## Física.3 -0.01024 0.06120 -0.167 0.86745
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5046 on 90 degrees of freedom
## (309 observations deleted due to missingness)
## Multiple R-squared: 0.6889, Adjusted R-squared: 0.6474
## F-statistic: 16.61 on 12 and 90 DF, p-value: < 2.2e-16Utilizamos o Residual standart error (RSE) para interpretar parte do nosso modelo. RSE é o desvio padrão dos resíduos que descreve a variabilidade referente ao modelo de regressão utilizado. Queremos que o valor RSE seja o menor possível. O RSE do modelo tem valor igual a 0.5046.
Uma segunda variável que utilizamos é o R-quadrado que apresenta valor referente ao coeficiente de determinação, ela varia entre 0-1 e indica quanto o modelo consegue explicar o valor observado, no nosso caso, o cra. Quanto maior o R-quadrado, melhor, significando que o modelo é mais explicativo. Existe uma tendência de que quanto mais variáveis o modelo possuir, maior o seu poder explicativo, incentivando a inserção de muitas variáveis e para combater isso existe o R-quadrado ajustado. R-quadrado ajustado funciona da mesma maneira que o R-quadrado, com a diferença de que ele sofre penalização se há inclusão de variáveis com muito pouco poder explicativo. Para todos os modelos deste documento estaremos utilizando valores relacionados ao R-quadrado ajustado para medir o poder de explicação dos mesmos.
Interpretando os dados acima temos que o R-quadrado ajustado tem valor igual a 0.6474, isso significa que 64.74% do cra consegue ser explicado pelas variáveis independentes presentes no modelo. Então, sim, o modelo explica parte da variável dependente em mais de 50%.
Todas as variáveis são úteis para o modelo de regressão?
Apesar de o modelo explicar a variável dependente em quase 67%, nem todas as variáveis independentes que fazem parte dele apresentam influência considerável. Neste documento, utilizaremos dois principais valores para avaliar a utilidade e significância de uma variável independente presente em um modelo: seu coeficiente (relacionado a magnitude) e p-valor.
O coeficiente de uma variável é referente ao poder de influência que ela tem na variável dependente. O p-valor é referente a probabilidade de existência por chance, queremos que este valor seja o menor possível para que a variável seja considerada importante para o modelo.
Disciplinas como Física 3, Cálculo 2, Cálculo 1 etc, apresentam baixo coeficiente e p-valor elevado. Essas variáveis influenciam minimamente e não são consideradas úteis para o modelo. Portanto, nem todas as variáveis são úteis para o modelo de regressão apresentado.
Se a resposta para a pergunta anterior foi não, construa um novo modelo sem essas variáveis e o compare ao modelo com todas as variáveis (e.g. em termos de R2 e RSE).
Selecionaremos variáveis baseadas em seus coeficientes e p-valor. Além disso, quando duas variáveis possuírem um alto coeficiente de correlação*, removeremos uma delas, já que váriáveis muito correlacionadas inserem redundância no modelo e podem proporcionar geração de valores incosistentes. Utilizaremos o *summary do modelo e o correlograma abaixo para extrair e analisar esses valores.
**Um valor será considerado alto quando for >= 0.65. Valor escolhido com base na comparação relativa de coeficientes obtidos.
M = cor(na.omit(graduados[,1:12]))
corrplot(M, type = "lower", title = "Correlação de disciplinas", order="hclust", col=brewer.pal(n=7, name="PuOr"), addCoef.col = "black", tl.col="black", tl.srt=45, mar=c(0,0,1,0) )
Iniciaremos removendo variáveis com alto coeficiente de correlação:
- O coeficiente de correlação de P1 e LP1 é igual a 0.77, decidimos manter P1 porque apresenta coeficiente (-0.02593) mais significativo e menor p-valor (0.73660).
- O coeficiente de correlação de P2 e Grafos é igual a 0.65, decidimos manter P2 porque apresenta coeficiente (0.29214) mais significativo e menor p-valor (0.00293).
- O coeficiente de correlação de LP2 e Discreta é igual a 0.65, decidimos manter Discreta porque apresenta coeficiente (0.23935) mais significativo e menor p-valor (9.63e-05).
Agora removemos as variáveis menos significativas considerando menores valores referentes ao coeficiente e maiores referentes ao p-valor:
- Cálculo.1 - coeficiente: 0.02121 / p-valor: 0.66661
- Cálculo.2 - coeficiente: -0.00100 / p-valor: 0.98499
- Física.3 - coeficiente: -0.01024 / p-valor: 0.86745
Sendo assim, nosso modelo fica da seguinte maneira:
graduados = graduados[, c("LPT", "P1", "IC", "Vetorial", "Discreta", "P2", "cra")]
rl = lm(cra ~ ., data = na.omit(graduados))
predicoes = predict.lm(rl ,graduados)
ggplot(graduados, aes(y=graduados$cra, x=predicoes)) +
geom_point(alpha = 0.5, position = position_jitter(width = 0.3), color="#a6761d") +
labs(title="Previsão do modelo", x= "", y="") +
geom_line(aes(y = predict(rl, graduados)), colour = "#e41a1c")
summary(rl)##
## Call:
## lm(formula = cra ~ ., data = na.omit(graduados))
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.26305 -0.24549 0.06888 0.34986 1.17262
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.07020 0.35305 3.031 0.002660 **
## LPT 0.09195 0.03479 2.643 0.008669 **
## P1 0.05407 0.03047 1.774 0.077052 .
## IC 0.19125 0.04939 3.872 0.000134 ***
## Vetorial 0.14360 0.02936 4.891 1.69e-06 ***
## Discreta 0.16460 0.03037 5.420 1.27e-07 ***
## P2 0.17707 0.03380 5.239 3.16e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5342 on 284 degrees of freedom
## Multiple R-squared: 0.6006, Adjusted R-squared: 0.5921
## F-statistic: 71.17 on 6 and 284 DF, p-value: < 2.2e-16O modelo agora apresenta um R-quadrado ajustado mais elevado, com valor igual a 0.5921, ou seja, ele explica em 59.21% a variável dependente. Por outro lado, o RSE teve seu valor elevado para 0,5342. Apesar disso, devido ao fato de que removemos variáveis, a quantidade de linhas com valores nulos diminuiu, aumentanto o tamanho da amostra e, consequentemente, a quantidade de graus de liberdade.
Analise os plots de resíduos de cada variável e veja se algum (um ou mais) deles indica não aleatoriedade dos erros.
Os plots abaixo são referentes aos resíduos de cada disciplina. Se obsevarmos bem, todos se comportam de maneira bem semelhante. Os resíduos estão bem espalhados em torno da reta em 0 e percebemos alguns outliers próximos ao valor -2. Não é possível notar a presença de nenhum padrão na formação dos plots, indicando que os resíduos são aleatórios, algo positivo.
ggplot(rl, aes(LPT, .resid)) +
labs(title="Resíduos do modelo para a disciplina LPT", x= "Nota", y="Resíduos") +
geom_point(alpha = 0.4, color="#1b9e77") +
geom_hline(yintercept = 0, colour = "#1f78b4")
ggplot(rl, aes(P1, .resid)) +
labs(title="Resíduos do modelo para a disciplina P1", x= "Nota", y="Resíduos") +
geom_point(alpha = 0.4, color="#d95f02") +
geom_hline(yintercept = 0, colour = "#1f78b4")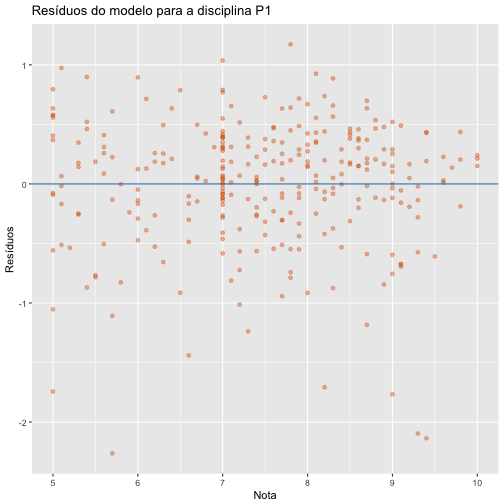
ggplot(rl, aes(IC, .resid)) +
labs(title="Resíduos do modelo para a disciplina IC", x= "Nota", y="Resíduos") +
geom_point(alpha = 0.4, color="#7570b3") +
geom_hline(yintercept = 0, colour = "#1f78b4")
ggplot(rl, aes(Vetorial, .resid)) +
labs(title="Resíduos do modelo para a disciplina Vetorial", x= "Nota", y="Resíduos") +
geom_point(alpha = 0.4, color="#e7298a") +
geom_hline(yintercept = 0, colour = "#1f78b4")
ggplot(rl, aes(Discreta, .resid)) +
labs(title="Resíduos do modelo para a disciplina Discreta", x= "Nota", y="Resíduos") +
geom_point(alpha = 0.4, color="#66a61e") +
geom_hline(yintercept = 0, colour = "#1f78b4")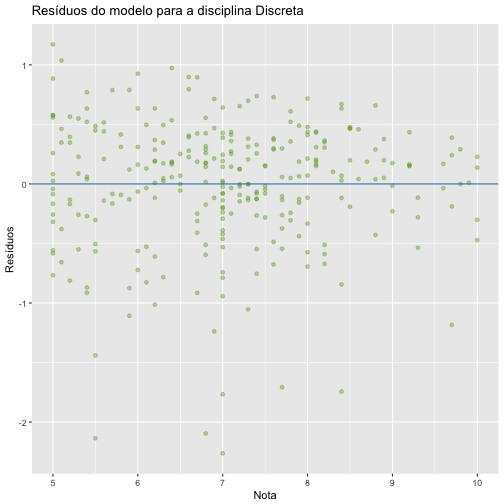
ggplot(rl, aes(P2, .resid)) +
labs(title="Resíduos do modelo para a disciplina LPT", x= "Nota", y="Resíduos") +
geom_point(alpha = 0.4, color="#e6ab02") +
geom_hline(yintercept = 0, colour = "#1f78b4")
Para complementar o comentário sobre os gráficos acima temos abaixo um gráfico que apresenta a frequência de resíduos. Os resíduos seguem uma distribuição normal de média 0, algo desejado para a representação de um bom modelo.
ggplot(rl, aes(.resid)) + labs(title="Frequência de resíduos para grupo do sexo feminino", x= "Resíduo", y="Frequência") +
geom_freqpoly(binwidth = 0.5, color="springgreen4")
Que período consegue explicar melhor o desempenho final (primeiro ou segundo)?
Com base no modelo anterior criado, geramos dois novos modelos de regressão linear para cada um dos semestre e comparamos seus valores de R-quadrado ajustado e RSE.
Semestre 1
Abaixo temos a criação do modelo para as disciplinas do primeiro semestre e seu gráfico mostrando os dados da amostra com relação a predição do modelo linear proposto. Logo após, os detalhes sobre o modelo.
graduados1 = graduados[,c("Vetorial", "LPT", "P1", "IC", "cra")]
graduados1 = na.omit(graduados1)
rl1 = lm(cra ~ ., data = graduados1)
predicoes1 = predict.lm(rl1 ,graduados1)
ggplot(graduados1, aes(y=graduados1$cra, x=predicoes1)) +
geom_point(alpha = 0.5, position = position_jitter(width = 0.3), color="#984ea3") +
labs(title="Previsão do modelo Semestre 1", x= "", y="") +
geom_line(aes(y = predict(rl1, graduados1)), colour = "#e41a1c")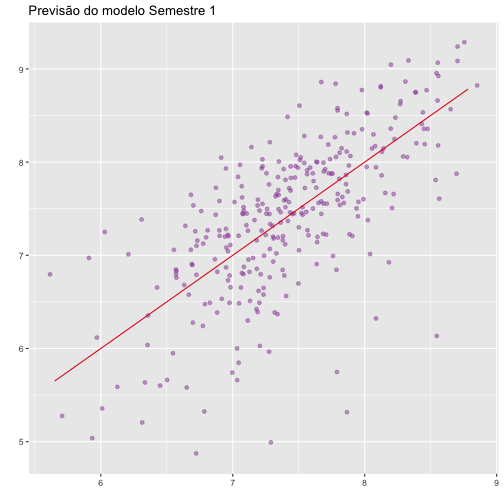
Nos detalhes abaixo concluímos que o modelo com disciplinas do primeiro período explica em 50.89% a variável dependente, pois o mesmo apresenta R-quadrado ajustado com valor igual a 0.5089. Já seu RSE é igual a 0.5841.
summary(rl1)##
## Call:
## lm(formula = cra ~ ., data = graduados1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.57648 -0.30289 0.08898 0.38674 1.22632
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.29320 0.37856 3.416 0.000724 ***
## Vetorial 0.15711 0.03145 4.996 1.00e-06 ***
## LPT 0.11576 0.03687 3.139 0.001864 **
## P1 0.14305 0.03010 4.752 3.15e-06 ***
## IC 0.35370 0.04865 7.270 3.23e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5841 on 296 degrees of freedom
## Multiple R-squared: 0.5154, Adjusted R-squared: 0.5089
## F-statistic: 78.71 on 4 and 296 DF, p-value: < 2.2e-16Semestre 2
Abaixo temos a criação do modelo para as disciplinas do segundo semestre e seu gráfico mostrando os dados da amostra com relação a predição do modelo linear proposto. Logo após, os detalhes sobre o modelo.
graduados2 = graduados[, c("Discreta", "P2", "cra")]
graduados2 = na.omit(graduados2)
rl2 = lm(cra ~ ., data = graduados2)
predicoes2 = predict.lm(rl2 ,graduados2)
ggplot(graduados2, aes(y=graduados2$cra, x=predicoes2)) +
geom_point(alpha = 0.5, position = position_jitter(width = 0.3), color="#fb8072") +
labs(title="Previsão do modelo Semestre 2", x= "", y="") +
geom_line(aes(y = predict(rl2, graduados2)), colour = "#e41a1c")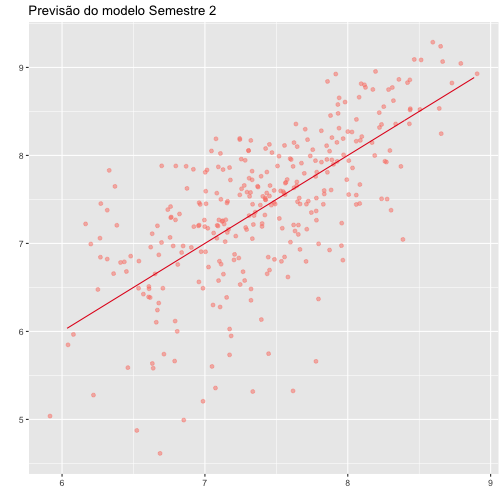
Nos detalhes abaixo concluímos que o modelo com disciplinas do segundo período explica em 46.03% a variável dependente, pois o mesmo apresenta R-quadrado ajustado com valor igual a 0.4603 Já seu RSE é igual a 0.6216.
summary(rl2)##
## Call:
## lm(formula = cra ~ ., data = graduados2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.3370 -0.3236 0.1042 0.3816 1.4854
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.15763 0.26422 11.951 < 2e-16 ***
## Discreta 0.29418 0.02995 9.821 < 2e-16 ***
## P2 0.28134 0.03258 8.634 3.03e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6216 on 314 degrees of freedom
## Multiple R-squared: 0.4637, Adjusted R-squared: 0.4603
## F-statistic: 135.8 on 2 and 314 DF, p-value: < 2.2e-16Conclusão
Considero que o modelo com variáveis relacionadas apenas ao primeiro período consegue explicar melhor o desempenho final de cada aluno porque, além de apresentar um maior R-quadrado ajustado (0.5089 > 0.4603), seu RSE é de menor valor (0.5841 < 0.6216).
Use o modelo para predizer o seu próprio desempenho e compare a predição com o seu CRA atual. Comente o resultado.
Utilizando o modelo inicial ajustados com disciplinas do primeiro e segundo período:
notas = data.frame(LPT = 8.2, P1 = 7.6, IC = 8.4, Vetorial = 7.3, Discreta = 7.1, P2 = 7.3)
predict(rl, notas)## 1
## 7.351167O modelo prediz que, de acordo com minhas notas, meu cra deverá ser 7.35. Meu cra atual é iqual a 7.45, valor bem próximo do previsto. Talvez faltem uma ou mais variáveis no modelo para ter um valor mais próximo do real, ou uma amostra maior. Outros fatores podem influênciar como inconsistência nos dados, o fato de que atualmente alunos podem optar por cursar ou não LPT no início do curso ou simplesmente porque meu cra atual ainda não sofreu todas as alterações das disciplinas que ainda faltam ser cursadas até a conclusão do curso, fato que está incluso nos dados utilizados para construir o modelo.