Uso de modelos de regressão com Ridge e Lasso

Apresentação dos dados

Como continuação da Parte 2, nesse fase estaremos criando modelos de regressão, comparando-os e realizando predição de dados. Continuamos trabalhando com disciplinas dos dois primeiros semestres para a criação de um modelo que consiga calcular o cra de uma determinada matrícula. Para isso dividimos os dados em treino, validação e teste.

Legenda

Cálculo.1: Cálculo Diferencial e Integral I - Período 1
Vetorial: Álgebra Vetorial e Geometria Analítica - Período 1
LPT: Leitura e Produção de Textos - Período 1
P1: Programação I - Período 1
LP1: Laboratório de Programação I - Período 1
IC: Introdução à Computação - Período 1
Cálculo.2: Cálculo Diferencial e Integral II - Período 2
Discreta: Matemática Discreta - Período 2
P2: Programação II - Período 2
LP2: Laboratório de Programação II - Período 2
Grafos: Teoria dos Grafos - Período 2
Física.3: Fundamentos de Física Clássica - Período 2

dados_treino = read.csv("p1p2.graduados_treino.csv")
dados_validacao = read.csv("p1p2.graduados_validacao.csv")
dados_teste = read.csv("test.csv")

colnames(dados_teste) = c("matricula", "Cálculo.1", "Vetorial", "LPT", "P1", "LP1", "IC", "Cálculo.2", "Discreta", "P2", "LP2", "Grafos", "Física.3")

dados_treino = dados_treino[,2:15]
dados_validacao = dados_validacao[,2:15]

head(dados_treino)

##                          Matricula Cálculo.1 Vetorial LPT  P1 LP1  IC
## 1 002b348d3bc88b68aa6ebd24cfc9d6a0       5.6      7.5 9.1 8.0 8.7 8.4
## 2 007961bf3929ae353c8585e6c09df369       6.7      8.5 8.6 7.1 7.6 7.7
## 3 00960ff73dd29b59f4432072c2219c04       7.0      5.6 6.5 7.3 8.5 7.5
## 4 00b6f55e3639c9d3b835751a39ca6309        NA      7.3  NA  NA  NA  NA
## 5 00eb58fa89c562efda118e64efab77a5       5.5      7.0 7.4 6.8 6.3 8.6
## 6 01fc383ae2c2cb3e69d844272a5ecac0       6.6      5.9 8.3 9.1 8.8 9.5
##   Cálculo.2 Discreta  P2 LP2 Grafos Física.3      cra
## 1        NA      9.2 7.7 8.6    7.2      9.6 8.109877
## 2        NA      5.0 5.7 8.0    7.0      7.8 6.975824
## 3        NA      5.3 5.6 8.1    7.9      7.0 6.057282
## 4       7.2       NA  NA  NA     NA       NA 7.766667
## 5        NA      6.7 7.9 9.0    6.1      7.1 7.693827
## 6        NA      6.1 6.8 9.0    5.3      7.3 6.722892

Percebemos que algumas notas de disciplinas estão com valores vazios. Para que não precisemos remover toda a linha do data frame, vamos realizar imputação de dados. Decidimos que os valores vazios em disciplinas serão substituídos pelo valor do cra de suas respectivas matrículas.

for(i in 1:nrow(dados_treino)){
  for(j in 1:ncol(dados_treino)){
    if(is.na(dados_treino[i,j])){
      dados_treino[i, j] = dados_treino$cra[i]
    }
    if(i <= nrow(dados_validacao)){
      if(is.na(dados_validacao[i,j])){
        dados_validacao[i, j] = dados_validacao$cra[i]
      }
    }
  }
}

head(dados_treino)

##                          Matricula Cálculo.1 Vetorial      LPT
## 1 002b348d3bc88b68aa6ebd24cfc9d6a0  5.600000      7.5 9.100000
## 2 007961bf3929ae353c8585e6c09df369  6.700000      8.5 8.600000
## 3 00960ff73dd29b59f4432072c2219c04  7.000000      5.6 6.500000
## 4 00b6f55e3639c9d3b835751a39ca6309  7.766667      7.3 7.766667
## 5 00eb58fa89c562efda118e64efab77a5  5.500000      7.0 7.400000
## 6 01fc383ae2c2cb3e69d844272a5ecac0  6.600000      5.9 8.300000
##         P1      LP1       IC Cálculo.2 Discreta       P2      LP2
## 1 8.000000 8.700000 8.400000  8.109877 9.200000 7.700000 8.600000
## 2 7.100000 7.600000 7.700000  6.975824 5.000000 5.700000 8.000000
## 3 7.300000 8.500000 7.500000  6.057282 5.300000 5.600000 8.100000
## 4 7.766667 7.766667 7.766667  7.200000 7.766667 7.766667 7.766667
## 5 6.800000 6.300000 8.600000  7.693827 6.700000 7.900000 9.000000
## 6 9.100000 8.800000 9.500000  6.722892 6.100000 6.800000 9.000000
##     Grafos Física.3      cra
## 1 7.200000 9.600000 8.109877
## 2 7.000000 7.800000 6.975824
## 3 7.900000 7.000000 6.057282
## 4 7.766667 7.766667 7.766667
## 5 6.100000 7.100000 7.693827
## 6 5.300000 7.300000 6.722892

Como resultado final e para uma apresentação dos dados antes a criação de modelos, podemos ver abaixo a tabela de correlação entre a variáveis.

M = cor(na.omit(dados_treino[,2:14]))

corrplot(M, type = "lower", title = "Correlação de disciplinas",  order="hclust", col=brewer.pal(n=7, name="PuOr"), addCoef.col = "black", tl.col="black", tl.srt=45, mar=c(0,0,1,0) )

plot of chunk unnamed-chunk-3

Modelo de regressão Ridge

Iniciaremos utilizando o método de regularização Ridge Regression, que suaviza atributos relacionados e que aumentam o ruído no modelo. Porque queremos encontrar o bom valor lambda para o modelo, utilizamos nos dados de treino a função train para escolher aquele com menor RMSE dentre 100 possíveis valores lambda.

set.seed(825)
fitControl <- trainControl(method = "cv",
                           number = 10)

lambdaGrid <- expand.grid(lambda = 10^seq(10, -2, length=100))

ridge <- train(cra~., data = dados_treino[,2:14],
               method='ridge',
               trControl = fitControl,
                tuneGrid = lambdaGrid,
               preProcess=c('center', 'scale')
)

Abaixo vemos a sequência de valores obtidos e uma representação gráfica do mesmo.

ridge

## Ridge Regression 
## 
## 511 samples
##  12 predictor
## 
## Pre-processing: centered (12), scaled (12) 
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 460, 461, 461, 460, 459, 459, ... 
## Resampling results across tuning parameters:
## 
##   lambda        RMSE       Rsquared   MAE      
##   1.000000e-02  0.4666691  0.7205067  0.3533620
##   1.321941e-02  0.4666576  0.7205613  0.3533882
##   1.747528e-02  0.4666553  0.7206293  0.3534281
##   2.310130e-02  0.4666746  0.7207123  0.3535139
##   3.053856e-02  0.4667386  0.7208104  0.3536408
##   4.037017e-02  0.4668891  0.7209215  0.3538404
##   5.336699e-02  0.4672012  0.7210388  0.3541924
##   7.054802e-02  0.4678056  0.7211484  0.3548253
##   9.326033e-02  0.4689280  0.7212263  0.3559141
##   1.232847e-01  0.4709501  0.7212350  0.3577424
##   1.629751e-01  0.4745053  0.7211219  0.3609009
##   2.154435e-01  0.4806172  0.7208214  0.3654819
##   2.848036e-01  0.4908814  0.7202617  0.3732596
##   3.764936e-01  0.5076614  0.7193782  0.3861417
##   4.977024e-01  0.5342141  0.7181299  0.4082041
##   6.579332e-01  0.5746033  0.7165155  0.4426444
##   8.697490e-01  0.6332700  0.7145812  0.4938157
##   1.149757e+00  0.7142690  0.7124167  0.5632882
##   1.519911e+00  0.8203771  0.7101393  0.6530969
##   2.009233e+00  0.9523370  0.7078718  0.7608911
##   2.656088e+00  1.1084045  0.7057216  0.8867547
##   3.511192e+00  1.2842648  0.7037675  1.0263318
##   4.641589e+00  1.4733720  0.7020545  1.1752311
##   6.135907e+00  1.6677309  0.7005976  1.3294585
##   8.111308e+00  1.8590149  0.6993891  1.4822005
##   1.072267e+01  2.0397497  0.6984067  1.6266907
##   1.417474e+01  2.2042385  0.6976208  1.7575687
##   1.873817e+01  2.3490101  0.6970001  1.8725307
##   2.477076e+01  2.4727655  0.6965148  1.9708844
##   3.274549e+01  2.5759678  0.6961382  2.0530252
##   4.328761e+01  2.6602781  0.6958478  2.1201178
##   5.722368e+01  2.7280095  0.6956248  2.1739676
##   7.564633e+01  2.7816953  0.6954543  2.2166214
##   1.000000e+02  2.8237972  0.6953241  2.2500547
##   1.321941e+02  2.8565400  0.6952251  2.2760463
##   1.747528e+02  2.8818396  0.6951498  2.2961308
##   2.310130e+02  2.9012901  0.6950926  2.3115730
##   3.053856e+02  2.9161862  0.6950492  2.3233975
##   4.037017e+02  2.9275607  0.6950163  2.3324254
##   5.336699e+02  2.9362266  0.6949914  2.3393029
##   7.054802e+02  2.9428176  0.6949725  2.3445334
##   9.326033e+02  2.9478239  0.6949582  2.3485060
##   1.232847e+03  2.9516228  0.6949474  2.3515205
##   1.629751e+03  2.9545032  0.6949392  2.3538060
##   2.154435e+03  2.9566861  0.6949330  2.3555381
##   2.848036e+03  2.9583396  0.6949283  2.3568503
##   3.764936e+03  2.9595916  0.6949248  2.3578448
##   4.977024e+03  2.9605395  0.6949221  2.3585977
##   6.579332e+03  2.9612570  0.6949201  2.3591675
##   8.697490e+03  2.9617999  0.6949185  2.3595988
##   1.149757e+04  2.9622108  0.6949174  2.3599251
##   1.519911e+04  2.9625217  0.6949165  2.3601721
##   2.009233e+04  2.9627569  0.6949158  2.3603589
##   2.656088e+04  2.9629349  0.6949153  2.3605002
##   3.511192e+04  2.9630695  0.6949149  2.3606072
##   4.641589e+04  2.9631714  0.6949147  2.3606881
##   6.135907e+04  2.9632484  0.6949144  2.3607493
##   8.111308e+04  2.9633067  0.6949143  2.3607956
##   1.072267e+05  2.9633508  0.6949141  2.3608306
##   1.417474e+05  2.9633842  0.6949141  2.3608571
##   1.873817e+05  2.9634094  0.6949140  2.3608771
##   2.477076e+05  2.9634285  0.6949139  2.3608923
##   3.274549e+05  2.9634429  0.6949139  2.3609038
##   4.328761e+05  2.9634539  0.6949139  2.3609125
##   5.722368e+05  2.9634621  0.6949138  2.3609190
##   7.564633e+05  2.9634684  0.6949138  2.3609240
##   1.000000e+06  2.9634731  0.6949138  2.3609277
##   1.321941e+06  2.9634767  0.6949138  2.3609306
##   1.747528e+06  2.9634794  0.6949138  2.3609327
##   2.310130e+06  2.9634814  0.6949138  2.3609344
##   3.053856e+06  2.9634830  0.6949138  2.3609356
##   4.037017e+06  2.9634842  0.6949138  2.3609365
##   5.336699e+06  2.9634851  0.6949138  2.3609372
##   7.054802e+06  2.9634857  0.6949138  2.3609378
##   9.326033e+06  2.9634862  0.6949138  2.3609382
##   1.232847e+07  2.9634866  0.6949138  2.3609385
##   1.629751e+07  2.9634869  0.6949138  2.3609387
##   2.154435e+07  2.9634871  0.6949138  2.3609389
##   2.848036e+07  2.9634873  0.6949138  2.3609390
##   3.764936e+07  2.9634874  0.6949138  2.3609391
##   4.977024e+07  2.9634875  0.6949138  2.3609392
##   6.579332e+07  2.9634876  0.6949138  2.3609392
##   8.697490e+07  2.9634876  0.6949138  2.3609393
##   1.149757e+08  2.9634877  0.6949138  2.3609393
##   1.519911e+08  2.9634877  0.6949138  2.3609393
##   2.009233e+08  2.9634877  0.6949138  2.3609394
##   2.656088e+08  2.9634877  0.6949138  2.3609394
##   3.511192e+08  2.9634878  0.6949138  2.3609394
##   4.641589e+08  2.9634878  0.6949138  2.3609394
##   6.135907e+08  2.9634878  0.6949138  2.3609394
##   8.111308e+08  2.9634878  0.6949138  2.3609394
##   1.072267e+09  2.9634878  0.6949138  2.3609394
##   1.417474e+09  2.9634878  0.6949138  2.3609394
##   1.873817e+09  2.9634878  0.6949138  2.3609394
##   2.477076e+09  2.9634878  0.6949138  2.3609394
##   3.274549e+09  2.9634878  0.6949138  2.3609394
##   4.328761e+09  2.9634878  0.6949138  2.3609394
##   5.722368e+09  2.9634878  0.6949138  2.3609394
##   7.564633e+09  2.9634878  0.6949138  2.3609394
##   1.000000e+10  2.9634878  0.6949138  2.3609394
## 
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was lambda = 0.01747528.

plot(ridge)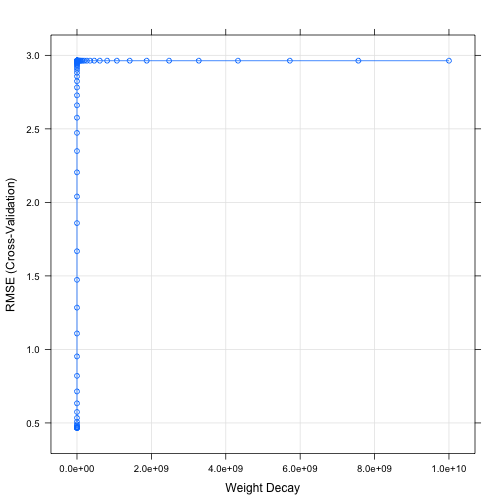

plot of chunk unnamed-chunk-5

Em seguida, realizamos a predição dos dados, mas agora utilizando os dados de validação. Abaixo temos um gráfico representando a validação do modelo, incluindo a “linha preditora” e resíduos.

ridge.pred <- predict(ridge, dados_validacao[,2:14])

ridge.pred <- data.frame(pred = ridge.pred, obs = dados_validacao$cra)

ggplot(ridge.pred, aes(x = pred, y = obs)) + geom_point(alpha = 0.5, position = position_jitter(width=0.2)) + geom_abline(colour = "darkred") + ggtitle("Previsão x Observado (validação)")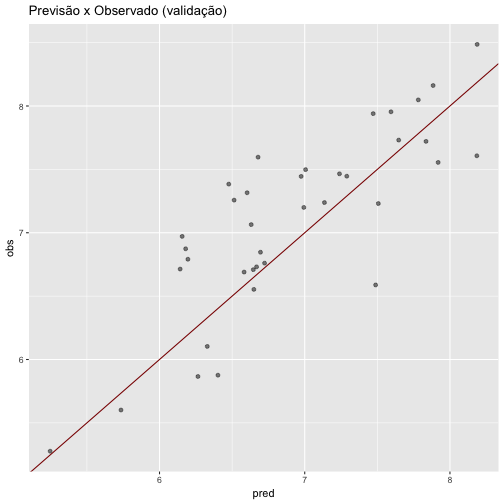

plot of chunk unnamed-chunk-6

O RMSE alto indica que o erro na predição foi alto. Ao utlizar a função round é fornecido que o RMSE obtido no modelo Ridge foi igual a 0.449.

round(defaultSummary(ridge.pred), digits = 3)

##     RMSE Rsquared      MAE 
##    0.450    0.667    0.378

Modelo de regressão Lasso

Assim como no tópico anterior, criaremos um novo modelo agora utilizando o método Lasso para a seleção de preditores. Após a criação e treinamento do modelo, também realizaremos a predição do mesmo.

lasso <- train(cra~., data = dados_treino[,2:14],
               method='lasso',
                tuneLength = 10,
               preProcess=c('center', 'scale')
)

O gráfico abaixo ilustra os 10 valores obtidos para fraction e a relação com seus respectivos RMSE. Em seguida os mesmos valores em detalhes.

plot(lasso)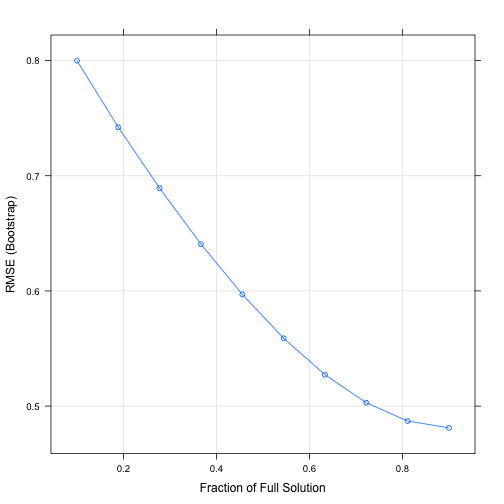

plot of chunk unnamed-chunk-9

lasso

## The lasso 
## 
## 511 samples
##  12 predictor
## 
## Pre-processing: centered (12), scaled (12) 
## Resampling: Bootstrapped (25 reps) 
## Summary of sample sizes: 511, 511, 511, 511, 511, 511, ... 
## Resampling results across tuning parameters:
## 
##   fraction   RMSE       Rsquared   MAE      
##   0.1000000  0.7998468  0.4808770  0.6355545
##   0.1888889  0.7420451  0.5357436  0.5889774
##   0.2777778  0.6891438  0.5912402  0.5451351
##   0.3666667  0.6406054  0.6288635  0.5039799
##   0.4555556  0.5970528  0.6547851  0.4666116
##   0.5444444  0.5589272  0.6726206  0.4332034
##   0.6333333  0.5272892  0.6846359  0.4048229
##   0.7222222  0.5029228  0.6929940  0.3818566
##   0.8111111  0.4870511  0.6985747  0.3649329
##   0.9000000  0.4811501  0.7005923  0.3577942
## 
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was fraction = 0.9.

Para realizar a predição dos dados também utilizamos os dados de validação. Abaixo temos um gráfico representando a validação do modelo, incluindo a “linha preditora” e resíduos.

lasso.pred <- predict(lasso, dados_validacao[,2:14])

lasso.pred <- data.frame(pred = lasso.pred, obs = dados_validacao$cra)

ggplot(lasso.pred, aes(x = pred, y = obs)) + geom_point(alpha = 0.5, position = position_jitter(width=0.2)) + geom_abline(colour = "darkred") + ggtitle("Previsão x Observado (validação)")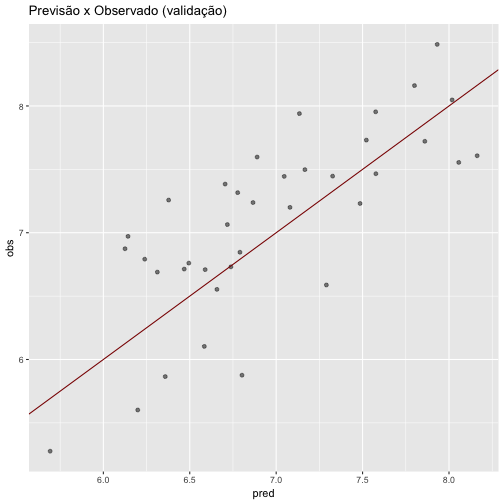

plot of chunk unnamed-chunk-10

Utilizando a função round é fornecido que o RMSE obtido no modelo Ridge foi igual a 0.437.

round(defaultSummary(lasso.pred), digits = 3)

##     RMSE Rsquared      MAE 
##    0.437    0.663    0.373

Comparação de modelos

Realizamos a comparação de modelos com base nos valores obtidos no RMSE. Quanto mais baixo o valor, melhor. Abaixo temos os gráficos mostrados anteriormente, agora lado a lado para uma melhor comparação.Vemos que o comportamento nos dados de validação é bem semelhante, os gráficos gerados não apresentam uma diferença perceptível muito significante.

compare <- ridge.pred
compare$model <- "Ridge"
lasso.pred$model <- "Lasso"

compare <- rbind(compare, lasso.pred)

ggplot(compare, aes(x = pred, y = obs)) + 
  geom_point(alpha = 0.5, position = position_jitter(width=0.2)) + 
  facet_grid(. ~ model) + 
  geom_abline() +
  ggtitle("Observado x Previsão (validação)")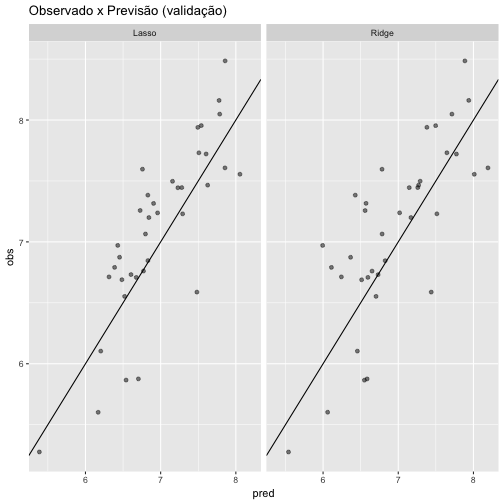

plot of chunk unnamed-chunk-12

Assim como nos gráficos, o fenômeno se repetiu para os valores de RSME. Ambos são altos e com quase o mesmo valor. Porém, o RMSE do modelo Lasso consegue atingir um menor valor. Podemos então considerar que o melhor modelo é o que utiliza da técnica Lasso. O melhor modelo é aquele que possui o RMSE mais baixo.

round(defaultSummary(ridge.pred), digits = 3)

##     RMSE Rsquared      MAE 
##    0.450    0.667    0.378

round(defaultSummary(lasso.pred), digits = 3)

##     RMSE Rsquared      MAE 
##    0.437    0.663    0.373

Importância de variáveis no modelo Lasso

Geramos uma representação gráfica com a importância das variáveis e mais abaixo estão os valores detalhados sobre a importância das mesmas. Vemos que Cálculo 2 é apresentada como a variável de maior importância, seguida por IC e P2. Temos apenas uma variável discartada que foi Física 3, apresentando overall igual a 0.

plot(varImp(lasso))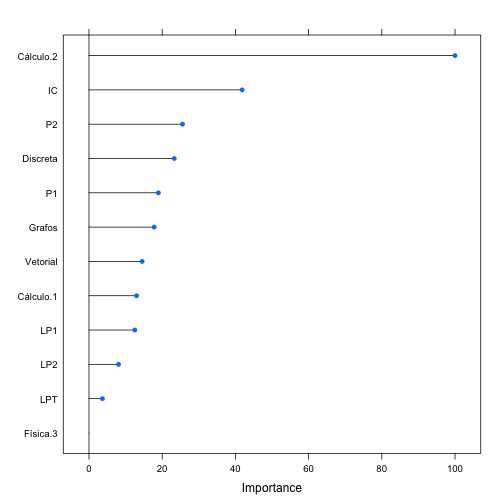

plot of chunk unnamed-chunk-14

varImp(lasso)

## loess r-squared variable importance
## 
##           Overall
## Cálculo.2 100.000
## IC         41.837
## P2         25.549
## Discreta   23.305
## P1         18.968
## Grafos     17.809
## Vetorial   14.513
## Cálculo.1  13.001
## LP1        12.518
## LP2         8.069
## LPT         3.667
## Física.3    0.000

Re-treino de modelo Lasso com dados de validação

Repetiremos aqui os passos realizados na construção e treino do modelo Lasso. Porém, desta vez estaremos utilizando os dados de validação para treinar o modelo. Segue:

lasso <- train(cra~., data = dados_validacao[,2:14],
               method='lasso',
                tuneLength = 10,
               preProcess=c('center', 'scale'))

O gráfico abaixo ilustra os 10 valores obtidos para fraction e a relação com seus respectivos RMSE. Em seguida os mesmos valores em detalhes.

plot(lasso)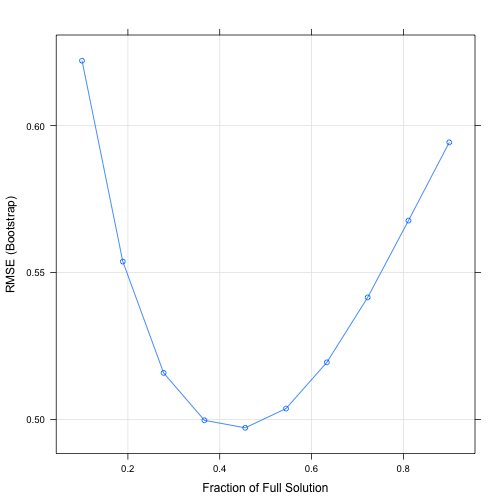

plot of chunk unnamed-chunk-16

lasso

## The lasso 
## 
## 37 samples
## 12 predictors
## 
## Pre-processing: centered (12), scaled (12) 
## Resampling: Bootstrapped (25 reps) 
## Summary of sample sizes: 37, 37, 37, 37, 37, 37, ... 
## Resampling results across tuning parameters:
## 
##   fraction   RMSE       Rsquared   MAE      
##   0.1000000  0.6221030  0.6100633  0.4834311
##   0.1888889  0.5537367  0.5910030  0.4262028
##   0.2777778  0.5158326  0.5758529  0.4060596
##   0.3666667  0.4996999  0.5693654  0.4061517
##   0.4555556  0.4971366  0.5642472  0.4115263
##   0.5444444  0.5037047  0.5587759  0.4191394
##   0.6333333  0.5194272  0.5493267  0.4324576
##   0.7222222  0.5415312  0.5363950  0.4502765
##   0.8111111  0.5676876  0.5190685  0.4702847
##   0.9000000  0.5943074  0.4995609  0.4909675
## 
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was fraction = 0.4555556.

Em seguida, a realização de predição utilizando os mesmos dados. Abaixo temos um gráfico representando a validação do modelo, incluindo a “linha preditora” e resíduos.

lasso.pred <- predict(lasso, dados_validacao[,2:14])

lasso.pred <- data.frame(pred = lasso.pred, obs = dados_validacao$cra)

ggplot(lasso.pred, aes(x = pred, y = obs)) + geom_point(alpha = 0.5, position = position_jitter(width=0.2)) + geom_abline(colour = "darkred") + ggtitle("Previsão x Observado (validação)")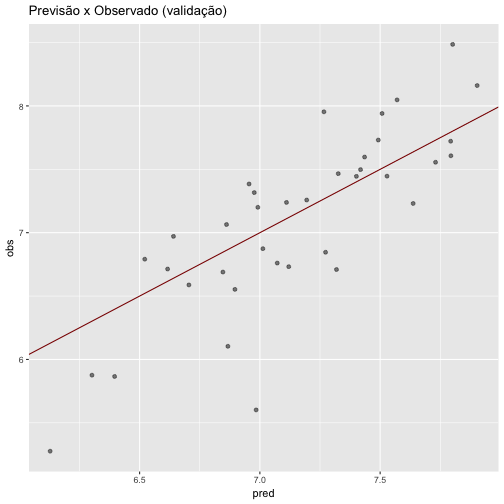

plot of chunk unnamed-chunk-17

Utilizando a função round é fornecido que o RMSE obtido no modelo Ridge foi igual a 0.454. Ao interpretar o resultado da função entendemos que houve um aumento no valor do RMSE e, consequentemente, uma piora no modelo.

round(defaultSummary(lasso.pred), digits = 3)

##     RMSE Rsquared      MAE 
##    0.416    0.718    0.327

Tentativa de melhora no modelo

Para tentar melhorar o modelo, vamos tentar uma nova abordagem para imputação de dados. Inicialmente, fazíamos a substituição de valores NA pelo valor do cra. Agora substituiremos esses valores vazios pela média das notas do primeiro período.

dados_treino = read.csv("p1p2.graduados_treino.csv")
dados_validacao = read.csv("p1p2.graduados_validacao.csv")

dados_treino = dados_treino[,2:15]
dados_validacao = dados_validacao[,2:15]

for(i in 1:nrow(dados_treino)){
  for(j in 1:ncol(dados_treino)){
    if(is.na(dados_treino[i,j])){
      dados_treino[i, j] = rowMeans(dados_treino[i,2:13], na.rm = T)
    }
    if(i <= nrow(dados_validacao)){
      if(is.na(dados_validacao[i,j])){
        dados_validacao[i, j] = rowMeans(dados_treino[i,2:13], na.rm = T)
      }
    }
  }
}

Assim como nos tópicos anteriores, criamos o modelo utlizando os dados de treino.

lasso <- train(cra~., data = dados_treino[,2:14],
               method='lasso',
                tuneLength = 10,
               preProcess=c('center', 'scale'))

O gráfico abaixo ilustra os 10 valores obtidos para fraction e a relação com seus respectivos RMSE. Em seguida os mesmos valores em detalhes.

plot(lasso)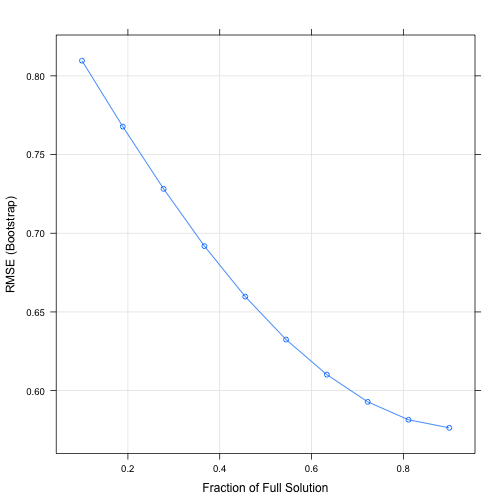

plot of chunk unnamed-chunk-21

lasso

## The lasso 
## 
## 511 samples
##  12 predictor
## 
## Pre-processing: centered (12), scaled (12) 
## Resampling: Bootstrapped (25 reps) 
## Summary of sample sizes: 511, 511, 511, 511, 511, 511, ... 
## Resampling results across tuning parameters:
## 
##   fraction   RMSE       Rsquared   MAE      
##   0.1000000  0.8096196  0.3734452  0.6392078
##   0.1888889  0.7677505  0.4348288  0.6037849
##   0.2777778  0.7282028  0.4739862  0.5707756
##   0.3666667  0.6918218  0.4994136  0.5405741
##   0.4555556  0.6597383  0.5162044  0.5132659
##   0.5444444  0.6324679  0.5286369  0.4891104
##   0.6333333  0.6101479  0.5380087  0.4682531
##   0.7222222  0.5928893  0.5457078  0.4510502
##   0.8111111  0.5814896  0.5509442  0.4381402
##   0.9000000  0.5763620  0.5537305  0.4309036
## 
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was fraction = 0.9.

Em seguida, a realização de predição utilizando os dados de validação. Abaixo temos um gráfico representando a validação do modelo, incluindo a “linha preditora” e resíduos.

lasso.pred <- predict(lasso, dados_validacao[,2:14])

lasso.pred <- data.frame(pred = lasso.pred, obs = dados_validacao$cra)

ggplot(lasso.pred, aes(x = pred, y = obs)) + geom_point(alpha = 0.5, position = position_jitter(width=0.2)) + geom_abline(colour = "darkred") + ggtitle("Previsão x Observado (validação)")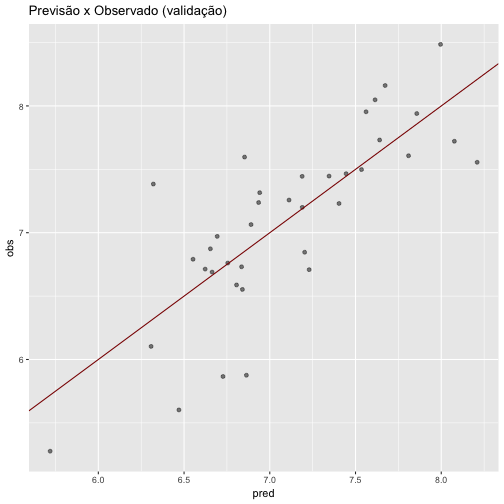

plot of chunk unnamed-chunk-22

Geramos uma representação gráfica com a importância das variáveis e mais abaixo estão os valores detalhados sobre a importância das mesmas. Vemos que Cálculo 2 continua sendo apresentada como a variável de maior importância, seguida por IC e agora Grafos. Temos apenas uma variável discartada que para o novo modelo foi LPT, apresentando overall igual a 0.

plot(varImp(lasso))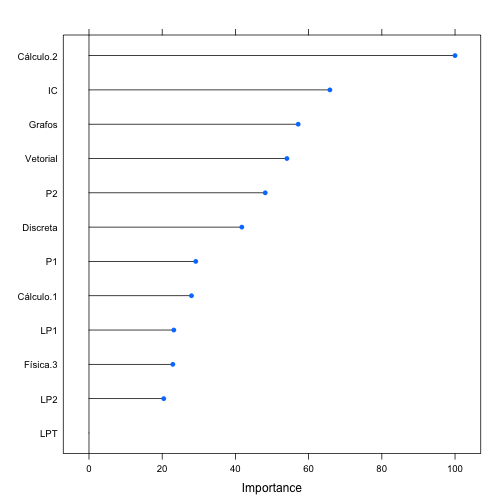

plot of chunk unnamed-chunk-23

varImp(lasso)

## loess r-squared variable importance
## 
##           Overall
## Cálculo.2  100.00
## IC          65.81
## Grafos      57.15
## Vetorial    54.07
## P2          48.15
## Discreta    41.75
## P1          29.17
## Cálculo.1   28.00
## LP1         23.17
## Física.3    22.91
## LP2         20.43
## LPT          0.00

Utilizando a função round é fornecido que o RMSE obtido no modelo Ridge foi igual a 0.411. Ao interpretar o resultado da função entendemos que houve uma diminuição no valor do RMSE e, consequentemente, uma melhora no modelo.

round(defaultSummary(lasso.pred), digits = 3)

##     RMSE Rsquared      MAE 
##    0.411    0.670    0.343

Gerando dados de predição

Para gerar dados de predição utilizamos dados de teste. Realizamos a predição de cra a partir das disciplinas dos dois primeiros semestres. O resultado foi submetido na plataforma Kaggle.

head(dados_teste)

##                          matricula Cálculo.1 Vetorial LPT  P1  LP1
## 1 037119c4740aa04d14742993e4aab789       8.2      9.1 8.3 7.0 10.0
## 2 0402a824ba0c87f73209cdb49b5072be       5.0      7.7 7.8 8.8  7.1
## 3 075d778a8444ef224757557479320148       5.2      5.0 9.6 7.8  6.2
## 4 09b9a1b335be033c236add2ba699c13f       7.6      6.0 8.7 7.0  8.4
## 5 0d3c0ddcdd2a97627575c27b5d1a058a       8.3      8.1 7.0 8.4  9.4
## 6 107f352e7c2d881c0f5f72a4584cd8fd       5.5      6.9 7.3 7.0  9.1
##    IC Cálculo.2 Discreta  P2 LP2 Grafos Física.3
## 1 7.7       9.2      9.7 9.2 8.9    9.1      9.0
## 2 8.8       7.3      7.3 7.1 7.3    8.0      6.0
## 3 5.4       5.1      5.0 5.7 7.0    7.0      9.3
## 4 7.0       5.0      5.9 7.8 6.0    6.6      5.9
## 5 8.4       7.8      7.9 8.5 8.5    8.0      8.0
## 6 7.4       7.0      7.6 9.4 5.2    8.4      8.8

dados_teste$cra = NA
dados_teste$cra = predict(lasso, dados_teste)
dados_teste = dados_teste[,c("matricula","cra")]
head(dados_teste)

##                          matricula      cra
## 1 037119c4740aa04d14742993e4aab789 8.309662
## 2 0402a824ba0c87f73209cdb49b5072be 7.380805
## 3 075d778a8444ef224757557479320148 6.478184
## 4 09b9a1b335be033c236add2ba699c13f 6.809691
## 5 0d3c0ddcdd2a97627575c27b5d1a058a 7.816722
## 6 107f352e7c2d881c0f5f72a4584cd8fd 7.552772